写在前面:
1.本文所有考点由老师在最后一节课进行期末考试复习时总结,并非考试大纲,所有考点仅供参考。
2.本文为您在Neijiang Normal University的数据结构课程期末复习提供一定帮助,如果您想获得高分,请多做题,光看这些总结是不够的。
3.请使用电脑,配合教材观看本文效果更佳。本文使用的教材是《数据结构教程(第5版)》李春葆。
4.转载本文请您附上链接。
5.请注意:本文在作者考试之前已经没有时间总结第十章:排序的考点,但这一章的内容是必考的,请师弟师妹们注意复习。
Copyright © 2020-2021 AnonyEast, All rights reserved.
试卷结构:单项选择题1分*30,填空题1分*10,判断题1分*10,程序填空题3分*10,分析应用题5分*4(单链表、二叉树、查找、排序)
第一章 绪论
以选择题和填空题出现
考点1 数据结构包含哪些方面
1.数据:描述客观事物的数和字符的集合。
2.数据元素:数据的基本单位。
3.数据项:具有独立含义的数据最小单位。
4.数据对象:性质相同的数据元素的集合,它是数据的一个子集。
5.数据结构:所有数据元素及数据元素之间的关系。
- 数据结构 = 数据 + 数据元素之间的关系
6.数据结构通常包括三个方面
- 逻辑结构:数据之间的逻辑关系。
- 存储结构(物理结构):数据元素及其关系在内存中的存储表示。
- 数据的运算:对数据施加的操作。
考点2 逻辑结构和物理结构
1.逻辑结构的类型:集合、线性结构(一对一)、树形结构(一对多)、图形结构(多对多)
2.物理结构的类型:顺序存储、链式存储、索引存储、哈希存储
3.重点掌握顺序存储和链式存储
(1)顺序存储结构
- 采用一组连续的存储空间存放所有数据元素
- 所有数据元素在存储器中占有一整块存储空间
- 两个逻辑上相邻的元素在存储器中的物理位置也相邻
- 优点:存储效率高;支持随机存取。
- 缺点:不便于数据修改,对元素的插入和删除需要移动一系列的元素。
(2)链式存储结构
- 每个元素用一个内存结点存储,每个结点单独分配。
- 所有的结点地址大概率不连续,因此无须占用一整块存储空间。
- 为了表示元素之间的逻辑关系,给每个结点附加指针域存放相邻结点的存储地址。
- 优点:便于数据修改,对元素插入和删除时仅需要修改指针域。
- 缺点:空间利用率低;不支持随机存取。
考点3 算法的特性和算法设计的目标
1.算法的5个重要特性
- 有穷性:不能无法结束。
- 确定性:相同的输入只能得到相同的输出。
- 可行性
- 有输入
- 有输出
2.算法设计的目标
- 正确性
- 可使用性
- 可读性:清晰第一,效率第二
- 健壮性
- 高效率域低存储量需求
考点4 时间复杂度和空间复杂度
1.算法时间复杂度:一种时间增长趋势分析。
2.算法空间复杂度:一个算法在运行过程中临时占用的存储空间大小的量度。
第二章 线性表
以填空题、程序填空题出现
考点1 线性表的特性
1.有穷性:有限个元素。
2.一致性:所有元素具有相同的数据类型。
3.序列性:存在唯一的开始元素和终端元素,除此之外,每个元素只有唯一的前驱元素和后继元素。
考点2 顺序表的基本运算
重点掌握插入元素和删除元素
1.顺序表的结构体
typedef struct
{
int data[MAXSIZE];
int length;
} SeqList;
2.插入数据元素的算法
(1)原理:要在表中第i个位置插入一个元素,则将顺序表第i个元素以及后面的每一个元素均向右边移动一位,并且从最后一位开始向右移动,全部移动完成后,将被插入元素赋值到第i个位置,最后顺序表长度+1。
int listInsert(SeqList *&L, int i, int e) //在顺序表第i个位置插入元素e
{
int j;
if (i < 1 || i > L->length || MAXSIZE == L->length) //i超出范围或表已经存满,返回0
{
return 0;
}
i--; //将顺序表逻辑序号转化为物理序号
for (j = L->length; j > i; j--) //将data[i]及后面的元素后移一个位置
{
L->data[j] = L->data[j - 1];
}
L->data[i] = e; //插入元素e
L->length++; //顺序表长度+1
return 1; //插入成功
}
(2)移动次数的计算
- n个元素,在第i个位置插入,则移动次数 = n - i + 1。
- i = 1时插入在开头,移动n次;i = n + 1时插入在末尾,移动0次。
- 平均移动次数 = n / 2
3.删除数据元素的算法
(1)原理:删除第i个元素,则将第i个元素后面的所有元素,均向左移动一个位置,这样就覆盖了第i个元素,实现了删除,最后将顺序表长度-1。
int listDeleteElementLocated(SeqList *&L, int i, int &e) //删除顺序表中的第i个元素,e用于接收被删除的元素
{
int j;
if (i < 1 || i > L->length) //乱传参数返回0
{
return 0;
}
i--; //将顺序表逻辑序号转换为物理序号
e = L->data[i];
for (j = i; j < L->length - 1; j++) //将data[i]之后的元素左移一个位置
{
L->data[j] = L->data[j + 1]; //把后面的赋值给前面的
}
L->length--; //顺序表长度减一
return 1; //删除成功返回1
}
(2)移动次数的计算
- 共n个元素,删除第i个元素,移动次数 = n - i
- i = 1时删除开头的元素,移动次数为n - 1;i = n时删除末尾的元素,移动次数为0。
- 平均移动次数 = (n - 1) / 2
4.其他算法参考(因为说了要考代码我就都放出来了,不一定都要掌握)
//初始化线性表
void initList(SeqList *&L)
{
L = (SeqList *)malloc(sizeof(SeqList)); //分配存放线性表的空间
L->length = 0; //置空线性表的长度为0
}
//创建线性表,元素个数为n
void createList(SeqList *&L, int a[], int n)
{
int i = 0;
L = (SeqList *)malloc(sizeof(SeqList)); //动态分配存放线性表的空间
while (i < n)
{
L->data[i] = a[i]; //将a[i]存放在L中
i++;
}
L->length = i;
}
//判断线性表是不是空表,0空1非空
int listEmpty(SeqList *L)
{
return !(0 == L->length);
}
//求线性表的长度
int listLength(SeqList *L)
{
return L->length;
}
//打印线性表各元素的值
void displayList(SeqList *L)
{
int i;
for (i = 0; i < L->length; i++)
{
printf("%d ", L->data[i]);
}
printf("\n");
}
//求线性表中第i个元素的值,e是接收结果的参数
int getElement(SeqList *L, int i, int &e)
{
if (i < 1 || i > L->length)
{
return 0; //传入的i不在正确范围的,返回0
}
e = L->data[i - 1]; //将第i个元素的值赋值给e
return 1;
}
//查找第一个与e相等的元素序号
int locateElement(SeqList *L, int e)
{
int i;
for (i = 0; i < L->length && e != L->data[i]; i++)
; //此循环查找元素e的位置
if (i >= L->length) //i==length时说明没有查找到
{
return 0;
}else{
return i + 1; //查找到返回元素序号
}
}
//以某个基准分区,左边小右边大
int listPartitionByBenchmark(SeqList *&L,int value)
{
if(value < 1 || value > L->length)
{
return 0;//乱传参数返回0
}
//benchmark记录基准值,i指向头元素,j指向尾元素
int benchmark = L->data[value - 1], i = 0, j = L->length - 1;
while(i < j)
{
while(j > i && L->data[j] > benchmark)//从右向左扫描,找到比基准小的就结束循环
{
j--;
}
L->data[i] = L->data[j];//把比基准小的那个元素放左边去
while(i < j && L->data[i] <= benchmark)//从左向右扫描,找到比基准大的就结束循环
{
i++;
}
L->data[j] = L->data[i];//把比基准大的那个元素放右边去
}
L->data[i] = benchmark;
return 1;//分区成功返回1
}
//将奇数移动到顺序表左边
void listOddNumberBeforeEvenNumber(SeqList *&L)
{
int i = 0, j = L->length - 1;
while(i<j)
{
while (j > i && 0 == L->data[j] % 2)//从右向左扫描,找到奇数结束循环
{
j--;
}
while(i < j && 0 != L->data[i] % 2)//从左向右扫描,找到偶数结束循环
{
i++;
}
if(i < j)//如果i<j说明可以换位置
{
swap(L->data[i], L->data[j]);
}
}
}
void swap(int &x,int &y)//交换函数
{
int temp = x;
x = y;
y = temp;
}
//倒置
void listInvertion(SeqList *&L)
{
int i = 0, j = L->length - 1;
while(i < j)
{
swap(L->data[i++], L->data[j--]);
}
}
考点3 顺序表和链表的区别以及各自的优缺点
一、顺序表和链表的区别
1.顺序表中,逻辑上相邻的元素对应的存储位置(物理位置)也相邻;链表每个结点的位置不必要求相邻。
2.顺序表没有指针域,链表有指针域。
3.插入或删除元素时,顺序表需要平均移动半个表的元素,链表只需要修改相关结点的指针域即可。
4.顺序表具有随机存取特性,链表不具有。
5.顺序表的存储密度等于1,链表小于1。
二、顺序表和链表的优缺点
1.顺序表的优缺点
优点: 存取速度快
缺点:
- 事先必须知道数组的长度
- 插入删除元素很慢
- 空间通常是有限制的
- 需要大块连续的内存块
- 插入删除元素的效率很低
2.链表的优缺点
优点:空间没有限制,插入删除元素很快
缺点:存取速度很慢
考点4 单链表(重要)
此部分要考代码,重点掌握插入和删除
带头结点的单链表结构如下
typedef struct LinkedListNode
{
int data; //数据域
struct ListNode *pNext; //指针域
} NODE;
一、插入和删除结点
插入和删除结点,我们必须明白一个原则——先连后断。在单链表中,无论插入还是删除,被操作结点的后继结点的地址一定不能丢,因为后继结点的地址如果丢失了,整个链表就连不起来了,因此一定要遵循先连后断的原则。
1.插入结点
我就简单叙述一下是怎么插入的:首先将被待插入位置的后继结点地址,赋值给新结点的指针域,这样就保留了后继结点的地址,然后将新结点的地址赋值给待插入位置的前置结点的指针域,这样就完成了插入操作。
以上叙述看不懂的话,建议大家自己看看下面的视频、然后画画图来理解。
视频链接: 插入结点(青岛大学-王卓)
用代码表示如下:把结点b插入到结点a的后面,这里提供两种方法,书上的方法是方法一
//方法一: //把a的下一个结点地址赋值给b的指针域,此时b的指针域指向a的下一个结点 b -> pNext = a -> pNext; //把b的地址赋值给a的指针域,此时a的指针域指向b,插入完成 a -> pNext = b; //方法二: //temp保存a的后继结点的地址 NODE* temp = a->pNext; //把新插入的结点地址赋值给a的指针域,此时a的指针域指向新插入的元素b a->pNext = b; //把temp的值赋值给b的指针域,这时候b的指针域指向插入前a的后继结点 q->pNext = temp;
2.删除结点
删除结点一样要先保留被删除位置的后继结点地址,因此我们将被删除位置的指针域中所保存的后继结点的地址,赋值给前置结点的指针域。则此时前置结点的指针域已经指向被删除结点的后一个结点了,删除完成。
以上叙述看不懂的话,建议大家自己看看下面的视频、画画图来理解。
视频链接: 删除结点(青岛大学-王卓)
用代码表示如下:删除结点a的后继结点
//temp保存被删除结点的地址 NODE* temp = a->pNext; //将被删除结点的后继结点地址赋值给结点a的指针域,此时a的指针域指向被删除结点的后继结点 a->pNext = temp -> pNext; //释放被删除结点 free(temp); //删除结点其实就是 //a->pNext = a->pNext->pNext; //不过这样只是断开与被删结点的连接,不会释放
二、创建单链表
尾插法算法:使尾指针始终指向新插入的结点
NODE *listCreateByTail(int array[], int len)//传入数组和数组长度
{
//分配了一个不存放有效数据的头结点
NODE *pHead = (NODE *)malloc(sizeof(NODE));
NODE *pTail = pHead; //生成始终指向尾结点的指针
for (int i = 0; i < len; i++)
{
//创建一个新的结点
NODE *pNew = (NODE *)malloc(sizeof(NODE));
pNew->data = array[i]; //把数据存放在新结点的数据域
pTail->pNext = pNew; //此时pTail指向插入前的尾结点,将新结点插入到pTail之后
pTail = pNew; //将pTail指向新结点
}
pTail->pNext = NULL; //写法二
return pHead;
}
头插法算法:使新插入的结点位于首结点(头结点的后继结点)
NODE *listCreateByHead(int array[], int len)//传入数组和数组长度
{
NODE *pHead = (NODE *)malloc(sizeof(NODE));
pHead->pNext = NULL;
for (int i = 0; i < len; i++)
{
NODE *pNew = (NODE *)malloc(sizeof(NODE));//创建新的结点
pNew->data = array[i];
//新结点指针域指向插入前的首结点,相当于插在了头结点之后
pNew->pNext = pHead->pNext;
//头结点指针域指向新插入的结点,这使得新插入的结点永远是首结点
pHead->pNext = pNew;
}
return pHead;
}
三、其他单链表算法
遍历
void listDisplay(NODE *pHead) //输出链表
{
NODE *p = pHead->pNext; //p指向首结点
while (NULL != p) //p不是NULL就输出
{
printf("%d ", p->data);
p = p->pNext; //打印完后p指向后继结点
}
printf("\n");
}
查找
//获取第position个结点的值,e用于接收结点的值
int getElement(NODE *pHead, int position, int &e)
{
int i;
NODE *p = pHead; //p指向头结点
if (position < 1) //乱传参数返回0
{
return 0;
}
for (i = 0; i < position && NULL != p; i++)
{
p = p->pNext;
}
if (p) //p不是空就赋值
{
e = p->data;
return 1; //获取成功返回1
}else{
return 0; //p为空返回0
}
}
清空(初始化)
void listInit(NODE *&pHead) //初始化链表
{
pHead = (NODE *)malloc(sizeof(NODE));
pHead->pNext = NULL;
}
销毁
void listDestroy(NODE *&pHead) //销毁链表
{
NODE *p = pHead->pNext, *pre = pHead; //pre指向p的前驱结点
while (NULL != p)
{
free(pre); //释放p的前驱结点
pre = p; //释放前驱结点后pre指向p
p = p->pNext; //p指向下一个结点
}
free(pre);
}
求长度
int listLength(NODE *pHead) //求链表长度
{
int count = 0;
NODE *p = pHead->pNext;
while (NULL != p)
{
count++;
p = p->pNext;
}
return count;
}
排序
//对链表从小到大排序,使用了选择排序
void listSort(NODE *pHead)
{
int i, j;
NODE *p, *q;
int len = listLength(pHead);
//i=0相当于数组第1个元素,则p = pHead->pNext相当于p指向链表的首结点
//i++相当于指向数组后一个元素,则p = p->pNext相当于指向p的下一个结点
for (i = 0, p = pHead->pNext; i < len - 1; i++, p = p->pNext)
{
//j=i+1相当于指向数组的i后面一个元素,则q = p->pNext相当于q指向p的下一个结点
for (j = i + 1, q = p->pNext; j < len; j++, q = q->pNext)
{
if (p->data > q->data) //相当于数组的a[i]>a[j]
{
swap(p->data, q->data);
}
}
}
}
删除结点
//删除第position个结点,用value接收其值
int listDelete(NODE *pHead, int position, int &value)
{
int i;
NODE *p = pHead;
for (i = 0; i < position - 1 && NULL != p; i++) //将p指向第i-1个结点
{
p = p->pNext;
}
if (NULL == p || i > position - 1 || position <= 0) //找不到i-1个结点返回0
{
return 0;
}
NODE *temp = p->pNext; //temp保存被删除的结点地址
p->pNext = temp->pNext; //第i-1个结点的指针域指向被删结点的下一个元素
value = temp->data; //将被删结点的值赋值给value
free(temp);
return 1; //删除成功返回1
}
插入结点
//在第position个结点左边插入一个值为value的结点
int listInsert(NODE *pHead, int position, int value)
{
int i;
NODE *p = pHead;
for (i = 0; i < position - 1 && NULL != p; i++) //将p指向第i-1个结点
{
p = p->pNext;
}
if (NULL == p || i > position - 1 || position <= 0) //找不到i-1个结点返回0
{
return 0;
}
NODE *pNew = (NODE *)malloc(sizeof(NODE)); //创建新结点
pNew->data = value;
//写法一
pNew->pNext = p->pNext; //把第i-1个结点指针域给新结点指针域
p->pNext = pNew; //把新结点地址赋值给第i-1个结点的指针域
/*写法二
NODE *temp = p->pNext;
p->pNext = pNew;
pNew->pNext = temp;
*/
return 1; //插入成功返回1
}
考点5:双链表
此部分只需要掌握双链表的优点。
1.与单链表的区别
每个结点包括一个指向后继结点的指针,和一个指向前驱结点的指针,所以当访问过一个结点后既可以依次向后访问每一个结点,也可以依次向前访问每一个结点。而单链表只能向后访问,不能向前访问。
考点6:有序表的归并算法
此部分考二路归并算法在最好和最坏情况下的比较次数,具体归并原理请看教材P67
两个长度分别为m、n的有序表A和B采用二路归并算法
最好情况:比较次数为MIN(m,n),即m、n中的较小值。
如:A = (1,2,3) B = (5,6,7,8,9),比较次数为3
最坏情况:比较次数为m + n - 1
如:A = (2,4,6) B = (1,3,5,7),比较次数为6
第三章 栈和队列
以选择题、填空题、判断题出现
考点1 栈的定义与特点
1.栈的特点:先进后出。从栈顶进栈,从栈顶出栈。
2.请务必看懂教材P79-80的例题3.1、3.2、3.3。
对栈的原理一知半解的,不知道进栈出栈是怎么回事的,上课在开飞机的……请看完下面这个视频,你就懂了,加油,奥利给——
视频链接:栈的定义和特点——数据结构与算法(青岛大学-王卓)
考点2 进栈与出栈
此部分考顺序栈的进栈与出栈
1.顺序栈的结构体
typedef struct
{
int data[MAXSIZE];//data数组存放栈中的数据元素,MAXSIZE为最大存储数量
int top; //栈顶指针,用于记录栈顶元素在data数组中的下标
} SqStack;
2.栈空栈满的条件
- 若指针s指向顺序栈
- 栈空:s -> top == -1
- 栈满:s -> top == MAXSIZE - 1(即data数组的最大下标)
3.进栈与出栈操作
- 元素e的进栈操作:先将栈顶指针top增加1,然后将元素e放在栈顶指针所指的位置。
- 出栈操作:先将栈顶元素赋值给元素e,然后栈顶指针top减去1。
考点3 共享栈
此部分主要考共享栈的4个要素
1.干嘛用的
如果需要用到两个相同类型的栈,若为他们各自单独开辟一块数组空间,则有可能出现第一个栈已满,而另一个栈还有很多空闲空间的情况。
为了解决这个问题,可以将两个栈合并,用一个数组来实现这两个栈,我们叫它共享栈。
2.特点
数组两端分别为两个栈的栈底,初始状态栈顶指针就在栈底,有元素进栈时,对应栈的栈顶指针向中间移动。
3.共享栈的4个要素
假设有两个栈,分别为栈1和栈2。
typedef struct
{
int data[MAXSIZE];//data数组存放栈中的数据元素,MAXSIZE为最大存储数量
int top1,top2; //两个栈的栈顶指针
} DStack;
- 栈空条件:栈1空为 top1 == -1,栈2空为 top2 == MAXSIZE
- 栈满条件:top1 == top2 - 1
- 元素e进栈:
- 进栈1操作为top1++;data[top1] = x
- 进栈2操作为top2--;data[top2] = x
- 出栈:
- 出栈1操作为x = data[top1];top1--
- 出栈1操作为x = data[top2];top1++
考点4 中缀表达式转换为后缀表达式
一、中缀表达式转换为后缀表达式
1.转换步骤
- 0.拿出铅笔、橡皮、草稿纸
- 1.首先,在不改变运算顺序的情况下,将每一个表达式都用括号括起来,由内向外括号依次变大。
- 2.从最大的括号开始去除,将两个表达式中间的运算符,移动到右括号的外面,然后用橡皮擦掉括号。
- 3.将每一个表达式按照从右向左的顺序,依次将运算符移动到右括号外,然后擦掉括号。
- 4.所有括号去除后,得到的式子便是后缀表达式。
2.视频讲解
以上步骤我承认我写的晦涩难懂,看看下面这个视频你就懂了。
视频链接:中缀转后缀表达式(逆波兰式)
考点5 队列的定义
1.队尾与对头
- 队尾:进行插入的一端。
- 队头:进行删除的一端。
- 队尾进队,对头出队。
2.特点:先进先出。
3.结构体
typedef struct
{
int data[MAXSIZE]; //data数组存放元素,MAXSIZE为最大存储数量
int front, rear; //队头指针和队尾指针记录数组下标
} CircularQueue;
考点6 顺序存储结构的循环队列(环形队列)
一、Why循环队列
循环队列解决了普通队列的假溢出问题,充分利用了队列空间。
二、进队与出队
1.初始状态:队尾指针rear和队头指针front都标记为0
2.元素e进队:先将rear增1,然后将元素e放在data数组中的rear位置,代码表示如下
//q是一个队列,e是入队元素 q->rear = (q->rear + 1) % MAXSIZE; q->data[q->rear] = e;
3.出队:先将front增1,然后取出data数组中的front位置的元素,代码表示如下
//q是一个队列,e用于接收出队的元素 q->front = (q->front + 1) % MAXSIZE; e = q->data[q->front];
三、队空队满的条件和元素个数
1.队空:q->rear == q->front,即队头指针和队尾指针指向同一位置,说明队列中没有元素。
2.队满:(q->rear + 1) % MAXSIZE == q->front,即队尾指针加1后,如果等于队头指针,说明此时队尾指针与队头指针相邻,队列已满。
注意:循环队列中任何时刻最多只能有MAXSIZE - 1个元素,牺牲了一个元素的空间。
3.队列中的元素个数 = (rear - front + MAXSIZE) % MAXSIZE
第四章 串
以选择题出现,考3分左右
考点1 串的基本概念
1.串:零个或多个字符组成的有限序列。
2.子串:一个串中任意个连续字符组成的序列。
例如"abcde"的子串有"a"、"ab"、"abc"、"abcd"、"bc"、"cde"等。
3.空串:不包含任何字符的串,长度为0,是任何串的子串。
考点2 BF算法、KMP算法
一、BF算法的时间复杂度
1.最好情况:主串的前m个字符恰好等于模式串的m个字符。此时时间复杂度为O(m)
2.最坏情况:时间复杂度(n*m)
二、KMP算法步骤
1.将模式串的所有前缀写出,例如模式串是ababc,则得到以下5个前缀
- a
- ab
- aba
- abab
- ababc
2.在写出的所有前缀中,找出每一个前缀的最长公共前后缀(不能是其自身)长度写在每个前缀前面。
例如,abab,长度为4,我们先写出其长度为3的前缀字符串,为aba,再写出其长度3的后缀字符串,为bab。很明显aba与bab不一致,则不存在长度为3的公共前后缀。接着,写出长度为2的前后缀字符串,分别为ab和ab,两个字符串一致,说明abab的最长公共前后缀的长度为2。将其记录在abab这个前缀的前面。
最后我们能得到这样的结果:
- 0 a
- 0 ab
- 1 aba
- 2 abab
- 0 ababc
3.看最左边的一列数字,我们去掉最后一个数字,在第一个数字前面添上一个-1,就得到了前缀表:-1 0 0 1 2
4.这个前缀表就是next数组
| j(数组下标) | 0 | 1 | 2 | 3 | 4 |
| t[j](字符数组) | a | b | a | b | c |
| next[j](前缀表) | -1 | 0 | 0 | 1 | 2 |
5.然后就是匹配过程,应该不会考。没有看懂以上步骤的小伙伴看下面这个视频。
视频链接:KMP字符串匹配算法
第五章 递归
考点1 递归应该满足的条件
1.需要解决的问题可以转化为一个或多个子问题来求解,而这些子问题的求解方法与原问题完全相同,只是在数量规模上不同。
2.递归的调用次数是有限的。
3.必须有结束递归的条件来终止递归。
考点2 递归出口和递归体
1.递归出口:递归到何时结束,指出明确的递归结束条件。
2.递归体:递归求解时的递推关系。
第六章 数组和广义表
以选择和填空题出现
考点1 数组的存储结构
一、一维数组的存储结构
1.按元素顺序存储到一块连续的内存单元中。
2.如果第1个元素的存储地址是1000,每个元素占用k个存储单元,则第n个元素的的存储地址是1000 + (n - 1)*k。
二、二维数组的存储结构
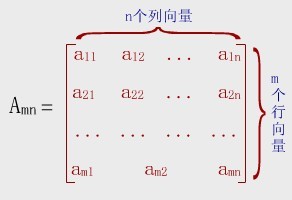
1.按行优先存放
将数组元素按行向量排列,第i+1个行向量紧接在第i个行向量后面。
【例】二维数组A[m][n]按行优先存储的线性序列为:
A[0][0]、A[0][1]…A[0][n]、A[1][1]、A[1][1]…A[1][n]…A[m][n]、A[m][1]…A[m][n]
C语言中的数组按行优先顺序存储。
2.按列优先存放
将数组元素按列向量排列,第i+1个列向量紧接在第i个列向量后面。
【例】二维数组A[m][n]按列优先存储的线性序列为:
A[0][0]、A[1][0]…A[m][0]、A[0][1]、A[1][1]…A[m][1]…A[m][1]、A[0][n]…A[m][n]
考点2 特殊矩阵的压缩存储
压缩存储:值相同的元素只分配一个空间,值为0的元素不分配空间。
一、对称矩阵的压缩存储
1.对称矩阵:元素值沿主对角线对称,即上三角的元素和下三角的元素是一样的。此时我们只需要存储上三角和主对角线的元素即可。共存储n(n+1)/2个元素
2.由于有接近一半的元素没有存储,但是我们需要根据行标和列标找到这些没有存储的元素的值,因此就需要解决如何根据行标和列标确定未存储元素在数组中的位置,我们记这个位置对应的数组下标为k。
3.其实要找k的值,就是要找你查找的元素,在上三角或者下三角中,按照从左往右,从上往下的顺序,是第几个元素(从0开始数,即a[0][0]是第0个元素)。
4.所以,我们查找元素a[i][j]
- 当i >= j时,说明元素在下三角或主对角线上,
- k = i(i+1)/2 + j
- 当i < j时,说明元素在上三角
- k = j(j+1)/2 + i
视频链接:对称矩阵的压缩存储(青岛大学-王卓)
二、上、下三角矩阵的压缩存储
1.上三角矩阵:只有上三角部分和主对角线的元素值不相同,下三角部分的元素值均为一个常数c。
2.下三角矩阵:只有下三角部分和主对角线的元素值不相同,上三角部分的元素值均为一个常数c。
3.这种矩阵只需要存储上三角或者下三角的元素即可,常数c放在数组最后,仅占用一个存储空间。总共存储n(n+1)/2 + 1个元素。
4.k的值,如果常数c在下三角,则
- 当i <= j时(上三角和主对角线元素),k = i(2n - i + 1)/2 + j - i
- 当i >j时(下三角常数c),k = n(n+1) / 2
如果常数c在上三角,则
- 当i < j时(上三角常数c),k = n(n+1) / 2
- 当i >= j时 (下三角和主对角线元素) ,k = i(i+1)/2 + j
视频链接: 上、下三角矩阵的压缩存储(青岛大学-王卓)
三、对角矩阵的压缩存储
k = 2i + j
考点3 三元组表和十字链表的优点
三元组表优点:非零元素在表中按行序有序存储,便于进行依次排序处理的矩阵运算。
三元组表缺点:无法随机存取,只能按顺序读取。
十字链表优点:灵活的插入因运算产生的新的非零元素;灵活的删除因运算产生的新的零元素。
考点4 广义表
广义表是线性表的推广,是有限个元素的序列,用括号表示法表示为:
GL = (a1,a2,a3...,ai,...,an),广义表中的元素,可以是原子或另一个广义表(子表)。
大写字母表示广义表,小写字母表示原子。
一、广义表的重要特性
- 1.广义表中的元素有相对次序。
- 2.长度:最外层包含元素的个数。
- 3.深度:所含括弧的层数,原子的深度为0,空表深度为1,递归表深度无穷。
- 4.广义表可以共享,一个广义表可以被其他广义表共享,称为再入表。
- 5.广义表可以是一个递归的表,一个广义表可以是自己的子表。递归表的深度无穷,长度有限。
二、判断一个广义表的表头、表尾、长度、深度
1.表头:第一个元素。
表尾:除了表头,其余元素构成的子表。因此表尾一定是一个广义表。
2.例题
- A = ( ) 空表,长度0,深度1,无表头表尾
- B = (( )) 长度1,深度2,表头为空表,表尾也为空表
- C = (a,(b,c)) 长度2,深度2,表头为原子a,表尾为子表((b,c))
- D = (x,y,z) 长度3,深度1,表头为原子x,表尾为子表(y,z)
- E = (C,D) 长度2,深度1,表头为子表C,表尾为子表(D)
- F = (a,F) 长度2,深度1,表头为原子a,表尾为子表(F)
- G = (a,(a,b),((a,b),c)) 长度3,深度4,表头为原子a,表尾为子表( (a,b),((a,b),c) )
3.总结:表头为第一个元素,表尾为剩下的元素然后加一对括号,表尾一定有括号,( )代表空表。长度就数有几个元素,深度就数有几对括号。
第七章 树和二叉树
重要,五种题型均有涉及
考点1 树的基本术语和树的性质
1.树的基本术语:如果你不知道结点的度、数的度是什么,如果你不知道数的深度(高度)是什么,如果你不知道什么叫孩子结点、双亲结点、兄弟结点、叶子结点,请务必看下面这个视频,否则将影响你做题。
视频链接:树的基本术语(青岛大学-王卓)
2.树的性质
性质1:树中的结点数等于所有结点的度数之和加1。
光这一个性质就可以出以下三种考题(多半以选择填空出现),而且出的可能性很高。教材P194的例7.2要看懂。
考题类型1:求总结点数。
总结点数 = 度为1的结点 * 1 + 度为2的结点 * 2 + 度为3的结点 * 3 + ... + 度为n的结点 * n + 1(根节点)
例题: 若一棵度为4的树中度为1、2、3、4的结点个数分别为4、3、2、2,则该树的总结点个数是多少?
- 解:度为1的结点数 * 1 = 4 * 1 = 4
- 度为2的结点数 * 2 = 3 * 2 = 6
- 度为3的结点数 * 3 = 2 * 3 = 6
- 度为4的结点数 * 4 = 2 * 4 = 8
- 总结点数:4 + 6 + 6 + 8 + 1(根节点) = 25
考题类型2:求叶子结点数。
叶子结点数 = 总结点数 - 度不为0的结点数
例题:某树度为4,且度为4、3、2、1的结点个数分别为1、2、3、4,则该树的叶子结点个数是多少?
- 解:先算总结点 = 4*1 + 3*2 + 2*3 + 1*4 + 1 = 21
- 去掉度不为0的结点,21 - 1 - 2 - 3 - 4 = 11
- 即叶子结点个数为11
考题类型3:求度为x的结点个数
这种题通常要设未知数
例题: 若一棵度为4的树中度为2、3、4的结点个数分别为3、2、2,总结点个数为25,则该树中度为1的结点个数是多少?
- 解:设度为1的结点个数是x,则
- x * 1 + 2*3 + 3*2 + 4*2 + 1 = 25
- 解得x = 4
- 所以度为1的结点个数为4
其他性质我估计不会考,就不写了。
考点2 满二叉树和完全二叉树
如果不知道满二叉树和完全二叉树,会影响二叉树的性质的解题
一、非空满二叉树
1.教材P199左上角的图就是满二叉树,所有分支结点都有左孩子和右孩子。
2.可以看到,满二叉树叶子结点都在最下面的一层。
3.满二叉树只有度为0和度为2的结点。
二、非空完全二叉树
1. 如果只是删除了满二叉树最底层最右边的连续若干个结点,这样形成的二叉树就是完全二叉树。
2.教材P199右上角的图就是完全二叉树,完全二叉树只有最下面两层的结点度数可以小于2,最下面一层的叶子结点依次排列在左边。
3.满二叉树是完全二叉树的一种特例。
4.叶子结点只可能在最下面两层中出现。此特点解题会用到。
5.如果有度为1的结点,只可能有1个,并且该结点只有左孩子没有右孩子。
考点3 二叉树的性质
性质1:非空二叉树上的叶子结点数等于双分支结点(度为2的结点)数加1。
性质2:二叉树的第i层上最多有2^(i-1)个结点。其实就是第1-7层分别最多有1 2 4 8 16 32 64个结点。
性质3:深度(高度)为h的二叉树最多有2^h-1个结点。其实就是假设每一层都是满的,把他们加起来。比如高度为5的二叉树最多有多少结点:1 + 2 + 4 + 8 + 16 = 31个结点。
教材P200例7.5要看懂。
考点4 二叉树的链式存储结构
看到链式存储就一脸懵逼的小伙伴,建议先看下面这个视频。
视频链接:二叉树的链式存储结构(青岛大学-王卓)
1.单个结点的标准存储结构示意图
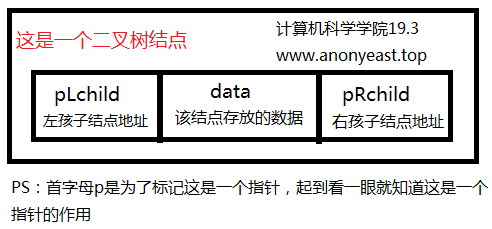
2.二叉树的结点用结构体表示如下
typedef struct BinaryTree
{
int data;
struct BinaryTree *pLchild;//左子树
struct BinaryTree *pRchild;//右子树
}BTNODE;
考点5 二叉树的遍历
此部分要考分析应用题:写出遍历序列,5分。要考递归遍历的代码。
一、先序遍历、中序遍历、后序遍历
1.遍历的顺序
- 先序遍历:根左右
- 中序遍历:左根右
- 后续遍历:左右根
2.已知二叉树写出三种遍历序列
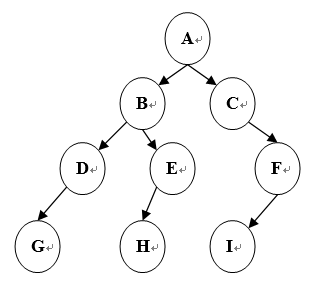
- 先序遍历顺序:A B D G E H C F I
- 中序遍历顺序:G D B H E A C I F
- 后序遍历顺序:G D H E B I F C A
不会遍历的同学,好好看视频哈
视频链接:遍历二叉树(青岛大学-王卓)
3.根据遍历序列确定二叉树
比如,已知先序和中序,求后序;已知中序和后序,求先序。这种题通常我们要先把二叉树还原出来,然后在写出要求的序列。
视频链接: 由遍历序列确定二叉树 (青岛大学-王卓)
二、三种遍历的递归算法
void preOrder(BTNODE *node) //先序遍历
{
if (NULL != node)//结点不为空则遍历
{
printf("%c ", node->data);//访问根节点
preOrder(node->pLChild); //遍历左子树
preOrder(node->pRChild); //遍历右子树
}
}
void inOrder(BTNODE *node) //中序遍历
{
if (NULL != node)//结点不为空则遍历
{
inOrder(node->pLChild); //遍历左子树
printf("%c ", node->data);//访问根节点
inOrder(node->pRChild); //遍历右子树
}
}
void postOrder(BTNODE *node) //后序遍历
{
if (NULL != node)//结点不为空则遍历
{
postOrder(node->pLChild); //遍历左子树
postOrder(node->pRChild); //遍历右子树
printf("%c ", node->data);//访问根节点
}
}
考点6 线索二叉树
线索二叉树将二叉树结点的空指针域利用起来,当某结点左指针域为空时,该指针域存储该结点前驱结点的地址,当某结点右指针域为空时,该指针域存储该结点后继结点的地址。
为了区分指针域究竟指向的是孩子还是前驱/后继结点,在结点的存储结构上增加两个标志位用来区分这两种情况。
- 左标志位:ltag = 0时,表示pLChild指向左孩子结点。
- ltag = 1时,表示pLChild指向前驱结点。
- 右标志位:rtag = 0时,表示pRChild指向右孩子结点。
- rtag = 1时,表示pRChild指向后继结点。
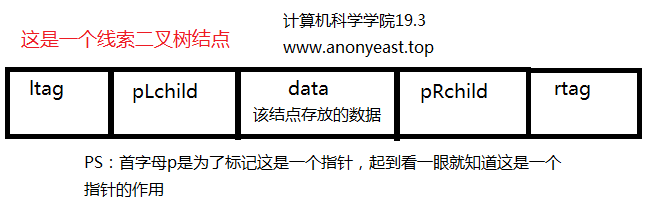
把教材P234的图能自己画出来,这部分就问题不大了。
视频链接: 线索二叉树 (青岛大学-王卓)
考点7 计算树的带权路径长度
一、 结点的带权路径长度
1.在许多应用中经常将树中的结点赋予一个有某种意义的数值,叫做该结点的权。
2.结点的带权路径长度 = 从根节点到该结点之间的路径长度 * 该结点的权。
二、 树的带权路径长度
1.树的带权路径长度 = 树中所有叶子结点的带权路径长度之和
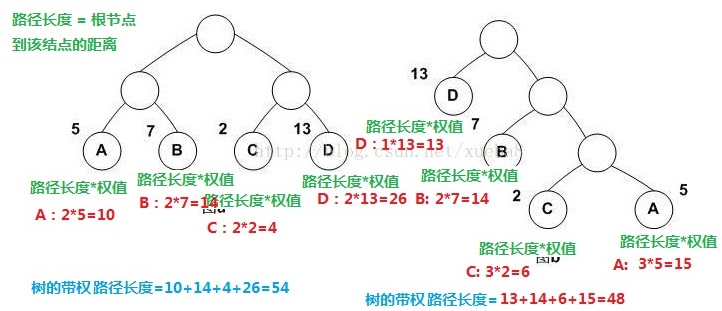
左边这棵树的带权路径长度为54,右边这棵树的带权路径长度为48。
考点8 哈夫曼树的构造算法
此部分只考哈夫曼二叉树的构造算法,不考哈夫曼三叉树或更多分支的树。
1.哈夫曼树:给定n个带权值的叶子结点构造一棵树,在树的度相同的情况下(例如只能造二叉树),树的带权路径长度最小的树,就是哈夫曼树。
2.特点:权值越大的叶子结点离根节点越近。
3.哈夫曼二叉树构造方法
使用贪心算法:构造哈夫曼树时优先选择权值小的结点。
- 步骤:1.构造森林全是根:把每个叶子结点都构造一棵树,这些树只有一个根节点。
- 2.选用两小造新树:将权值最小的两棵树作为左右子树,造一棵新的二叉树。
- 3.删除两小添新树:删除原来权值最小的两棵树,将造出来的新二叉树放在森林中。
- 4.重复23直到只剩一棵树,此时哈夫曼二叉树构造完成。
视频链接: 哈夫曼树的构造算法 (青岛大学-王卓) 有基础的可以从5分钟开始看
第八章 图
以选择题、填空题、判断题出现
考点1 图的定义和基本术语
此部分会在填空题和判断题出现
一、图的定义
1.图:G = ( V , E ) V是顶点的集合,E是边的集合。
2.无向图:两个顶点之间没有方向。边用小括号()表示。
3.有向图:两个顶点之间有方向。边用尖括号<>表示。
4.完全图:任意两个顶点都存在一条边相连。
二、图的基本术语
图的基本术语很多,最好根据下面这两个视频,把教材P254-257的内容熟悉一遍。这里我就不添加bilibili播放器代码了,因为内嵌播放器无法调节倍速,大家自己点击链接进去观看吧。
视频链接:图的定义和术语1(青岛大学-王卓)
视频链接:图的定义和术语2(青岛大学-王卓)
考点2 图的邻接矩阵(数组)存储
一、不带权图的邻接矩阵表示法
1.建立一个顶点表——记录各个顶点的信息,建立一个邻接矩阵——记录各个顶点之间的关系。
2.设图A = ( V , E )有n个顶点,则有顶点表Vexs[n]存储如下
| i | 0 | 1 | 2 | ... | n-1 |
| Vexs[i] | V1 | V2 | V3 | ... | VN |
有邻接矩阵是一个二维数组A.arcs[n][n],定义为:
如果 <i,j> 包含于E(有向图)或者(i,j)包含于E(无向图),则A.arcs[i][j]=1,否则 A.arcs[i][j]=0
代表存在顶点i到顶点j的边或者弧,则邻接矩阵中存储为1,否则存储为0。
3.例如下面这个无向图
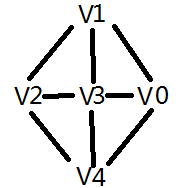
可以看到,V0到V0没有边连接,我们在坐标(V0,V0)处填写0,V0到V1有边连接,我们在坐标(V0,V1)处填写1,以此类推,两个顶点直接相连接,就填写1,不相连就填写0。因此,该图的邻接矩阵如下表所示。
| V0 | V1 | V2 | V3 | V4 | |
| V0 | 0 | 1 | 0 | 1 | 1 |
| V1 | 1 | 0 | 1 | 1 | 0 |
| V2 | 0 | 1 | 0 | 1 | 1 |
| V3 | 1 | 1 | 1 | 0 | 1 |
| V4 | 1 | 0 | 1 | 1 | 0 |
从以上无向图邻接矩阵可以观察到以下特点
- (1)无向图的邻接矩阵是对称的,因此存储的时候可以采用压缩存储的思想,只存储上三角部分或者下三角部分元素。
- (2)找顶点Vi的度,只需要看其所在的行,有多少个1,就是该顶点的度。
4.再看下面这个有向图
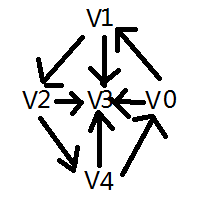
可以看到,V0到V0没有边连接,我们在坐标(V0,V0)处填写0,V0到V1有边连接且V0指向V1,我们在坐标(V0,V1)处填写1,但V1到V0虽然连接却并没有由V1指向V0,所以在坐标 (V1,V0) 填写0,以此类推,两个顶点相连接且满足前一个顶点指向后一个顶点,就填写1,否则填写0。因此,该图的邻接矩阵如下表所示。
| V0 | V1 | V2 | V3 | V4 | |
| V0 | 0 | 1 | 0 | 1 | 0 |
| V1 | 0 | 0 | 1 | 1 | 0 |
| V2 | 0 | 0 | 0 | 1 | 1 |
| V3 | 0 | 0 | 0 | 0 | 0 |
| V4 | 1 | 0 | 0 | 1 | 0 |
从以上有向图邻接矩阵可以观察到以下特点
- (1)第Vi行的含义:结点Vi的出度;第Vi列的含义:结点Vi的入度。
- (2)有向图的邻接矩阵不一定对称
- (3)顶点Vi的出度 = 第Vi行1的个数。
- (4)顶点Vi的入度 = 第Vi列1的个数。
二、带权图的邻接矩阵表示法
带权图的的邻接矩阵与不带权图的邻接矩阵区别就在于,每条边上多了一个权值,因此我们只需要将邻接矩阵中的1,修改为对应的权值即可,将邻接矩阵中的0,修改为无穷,其中自身到自身仍然保持0。
如下面这个带权有向图
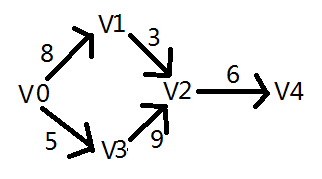
它的邻接矩阵表示如下
| V0 | V1 | V2 | V3 | V4 | |
| V0 | 0 | 8 | 无穷 | 5 | 无穷 |
| V1 | 无穷 | 0 | 3 | 无穷 | 无穷 |
| V2 | 无穷 | 无穷 | 0 | 无穷 | 6 |
| V3 | 无穷 | 无穷 | 9 | 0 | 无穷 |
| V4 | 无穷 | 无穷 | 无穷 | 无穷 | 0 |
考点3 图的邻接表存储
一、图的邻接表存储方法
1.图的邻接表是一种顺序与链式结合的存储方法。
2.在邻接表中有两种类型的结点:头结点和边结点。
- 头结点:用来存储顶点的数据(比如顶点的名称)和该顶点连接的第一条边结点的地址。每一个顶点对应一个头结点,所有的头结点存放在同一个数组中。
- 边结点:用来存储该边的邻接点的编号(对应头结点的数组下标)、下一条边的指针和该边的数据(比如权值)。
3.具体存储原理我自己都写不清楚,看下面这个视频可以大彻大悟
视频链接: 邻接表(青岛大学-王卓)
二、邻接表的特点
1.邻接表的表示不唯一。因为每个顶点对应的单链表中各边结点的次序是可以变换的。
2.对于n个顶点和e条边的无向图,邻接表有n个头结点和2e个边结点;
对于有n个顶点和e条边的有向图,其邻接表有n个头结点的e个边结点。
3.无向图,邻接表中顶点Vi的度,就是数其对应的单链表有几个边结点。
4.有向图,邻接表中顶点Vi的出度, 就是数其对应的单链表有几个边结点;
入度,则要遍历整个邻接表,查找有多少个边结点存放的顶点编号为i。
考点4 邻接矩阵和邻接表的区别
一、邻接矩阵的优缺点
1.优点
- 很容易判断任意一对顶点是否存在着边
- 方便查找任意一个顶点的邻接点(找是不是非零元素)
- 方便计算任意顶点的度
2.缺点
- 不便于增加或删除顶点
- 浪费空间:元素个数只取决于定点个数,无论边的数目是多少,其存储空间都为O(n²),因此存储稀疏图(点很多边很少)时,有大量无效元素
- 浪费时间:统计图中有多少条边时,无论有多少条边,都要全部遍历一遍,时间复杂度始终为O(n²),这会使存储稀疏图时十分浪费时间。
二、邻接表的优缺点
1.优点
- 方便找任意结点的所有邻接点
- 节约稀疏图的空间: 对于n个顶点和e条边的无向图,需要n个头结点,2e个边结点。不像邻接矩阵,与边的条数无关。
- 方便计算无向图任意顶点的度,和有向图任意顶点的出度(入度需要建立逆邻接表)。
2.缺点
- 不容易判断任何一对顶点是否有边连接,需要遍历整个邻接表。而邻接矩阵很容易。
三、邻接矩阵和邻接表的关系
1.联系:邻接表中每个链表对应于邻接矩阵中的一行,链表中的结点个数等于邻接矩阵一行中的非零元素个数。
2.区别
- (1)对于任意一个确定的无向图,邻接矩阵是唯一的(行列号与顶点编号一致),但邻接表不唯一(链接次序与顶点编号无关,与插入算法有关)
- (2)邻接矩阵的空间复杂度:O(n²),邻接表的空间复杂度O(n+e)
- (3)邻接矩阵多用于稠密图,邻接表多用于稀疏图。
考点5 广度优先遍历(BFS)和深度优先遍历(DFS)
一、广度优先遍历(BFS)
广度优先,就是一层一层的来,优先遍历一个结点的所有邻接点。BFS的实质是队列。
如下面这个图
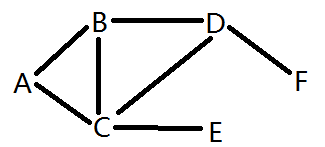
假设我们的遍历起点是B点,则BFS的遍历步骤是:
1.写出B点,然后访问B点的所有邻接点,有A、C、D,写出来,顺序无所谓。写完后,B点的所有邻接点已经访问完成,用绿色标记。
B A C D
2.接下来访问A点的所有邻接点,A点的所有邻接点为B、C,均已经写过了,则什么也不写。则A点的所有邻接点已经访问完成,用绿色标记。
B A C D
3.访问C点的所有邻接点,C点的所有邻接点为A、B、D、E,只有E点没有写过,写出来。此时C点的所有邻接点访问完成,用绿色标记。
B A C D E
4.访问D点的所有邻接点,有B、C、F,只有F点没有写过,写出来。此时D点的所有邻接点遍历完成,用绿色标记。
B A C D E F
5.按理说我们应该继续看E点和F点的邻接点,但是很明显这里已经把6个点全部写出来了,所以我们可以不继续往下看了。
6.得到以B点为起点的一个广度优先遍历序列:B A C D E F
注意事项:广度优先遍历的序列不唯一,得到的序列与起点和访问顺序有关,比如在第一步当中,如果我们把A、C、D的顺序写成A、D、C,则会得到另一个序列。只要你方法正确,即使写出来的序列不同,也是正确的。
二、深度优先遍历(DFS)
深度优先,就是一条路走到底,走到头了再折回来找别的路走,直到走完整个图。深度优先遍历需要用到栈来操作。
还是以下面这个图为例
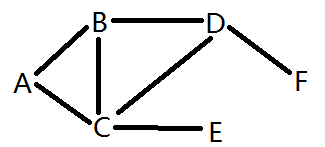
假设我们的遍历起点是B点,则DFS的遍历步骤是: (我直接用画图写的)
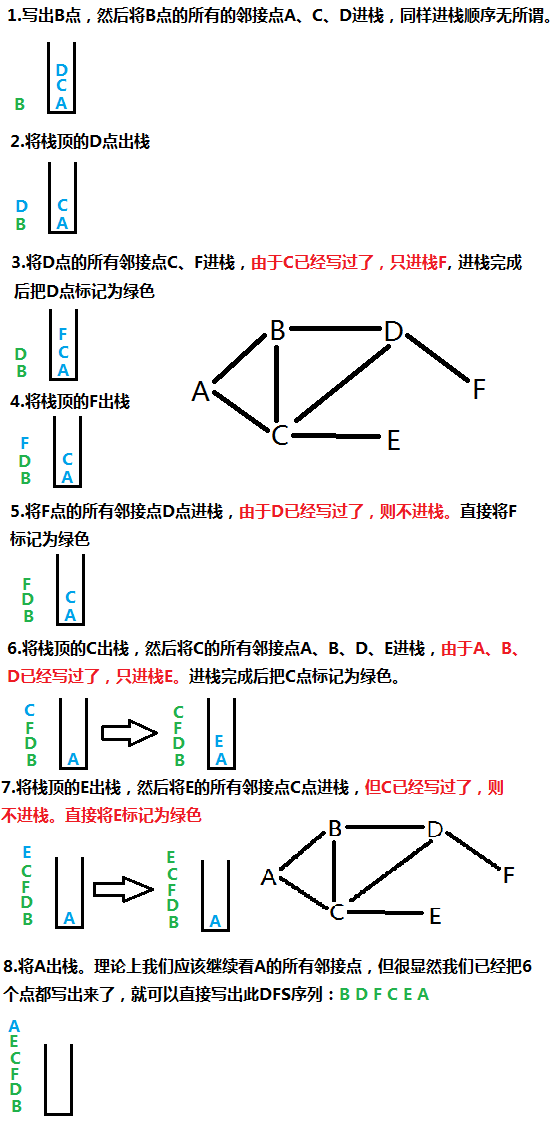
注意事项:深度优先遍历的序列同样不唯一,得到的序列与起点和访问顺序有关。比如在第一步当中,如果的进栈顺序是A、C、D,如果改成A、D、C的顺序,则会得到另一个序列。只要你方法正确,即使写出来的序列不同,也是正确的。
也可以听一听这个小哥哥讲解。
视频链接:BFS和DFS算法
考点6 拓扑排序
此部分可能考应用分析题:写出拓扑排序序列
一、排序方法
1.从有向图中选择一个没有前驱的顶点写出来。
2.从图中删除该顶点和该顶点发出的全部有向边。
3.重复上面两步直到图中不再存在没有前驱的顶点。
视频链接: 拓扑排序(青岛大学-王卓) 直接从14分钟开始看
第九章 查找
以填空题、算法填空题、分析应用题出现
考点1 顺序查找
一、应用范围
1.顺序表或线性链表表示的静态查找表。
2.表内元素之间无序。
二、查找思路
1.从表的一端向另一端逐个将元素的关键字和给定值k比较,若相等,则查找成功,返回该元素在表中的位置;若整个表扫描完后,都没有找到与k相等的值,则查找失败。
2.代码如下:在一个数据类型为int,数组长度为n的数组array中,查找值为k的元素,查找成功返回元素在数组中的逻辑序号,否则返回0。
//参数:array[]:传入的要查找的数组 n:数组的长度(元素个数) k:被查找的值
int sequentialSearch(int array[],int n,int k)
{
for(int i = 0; i < n; i++)//扫描整个数组
{
if(k == array[i])//如果找到第i个元素等于k,返回逻辑序号
{
return i + 1;
}
}
return 0;//上面的循环执行完了说明没找到,返回0
}
//书上的代码是这样的,写的可真烂啊
int SeqSearch(int array[],int n,int k)
{
int i = 0;
while(i < n && array[i] != k)//从表头往后找,不相等就递增i
{
i++;
}
if(i >= n) //i>=n说明已经扫描完了整个数组,没有找到等于k的
{
return 0;
}else{
return i+1;//找到了就返回逻辑序号
}
}
三、性能和优缺点
平均查找长度: (n + 1)/2 次
时间复杂度: O(n)
优点:算法简单,对表的结构没有特殊要求。
缺点:效率低,数组元素个数较多时不适合本算法。
考点2 折半查找(二分查找)
一、应用范围和特点
1.应用范围:必须是有序表。
2.特点:每次将待查找元素所在区间缩小一半。
二、查找思路
查找思路和猜数字差不多,每次缩小一半的范围。
具体查找原理用文字不太好描述,建议直接看教材P317,看不懂的看下面这个视频。
视频链接: 折半查找(青岛大学-王卓)
代码如下:在一个数据类型为int,数组长度为length的数组array中,查找值为k的元素,查找成功返回元素在数组中的逻辑序号,否则返回0。
int binarySearch(int array[],int length,int k)
{
int low = 0,high = length - 1,mid;//low初始为0,high初始为最大下标
while(high >= low)//如果low比high还大了,说明没找到
{
mid = (low+high)/2;//mid初始为中点值(low+high)/2
if(array[mid] == k)//查找的元素k等于中点,则找到了,返回数组下标+1
{
return mid + 1;
}
else if(k > array[mid]) //查找的元素k大于中点,说明在中点右边,需要修改low的值
{
low = mid + 1;
}
else //查找的元素k小于中点,说明在中点左边,需要修改high的值
{
high = mid - 1;
}
}
return 0; //如果上面的循环执行完了,说明没找到,返回0
}
考点3 二叉排序树
此部分教材P329例题9.3要看懂,不考代码
一、二叉排序树特点
1.根节点的左子树如果不为空,则左子树所有结点都要小于根节点。
2. 根节点的右子树如果不为空,则右子树所有结点都要大于根节点。
3.根节点的左右子树,又各自构成一棵二叉排序树。
二、根据已知序列画出二叉排序树
1.如果已经给出指定的序列,我们只需要按照"比根节点小的元素放左子树,比根节点大的元素放右子树,每一个根节点左边不能有比他自己还要大的元素,每一个根节点右边不能有比他自己还要小的元素"的原则,进行画图。
2.具体如何操作看下面这个视频
视频链接: 二叉排序树的生成(青岛大学-王卓) 从4分钟开始看
三、计算二叉排序树的平均查找长度
1.查找成功的平均查找长度
先把二叉排序树画出来,然后计算每一层的比较次数(某一层比较次数 = 该层是第几层 * 结点个数),最后将每一层的比较次数相加,除以结点个数,就是查找成功的平均查找长度。
例如教材P329图9.11(a)
- 第一层:1(第1层) * 1(1个结点) = 1
- 第二层:2(第2层) * 2(2个结点) = 4
- 第三层:3 * 3 = 9
- 第四层:4(第4层) * 3(3个结点) = 12
- 第五层:5(第5层) * 2(2个结点) = 10
- 第六层:6(第6层) * 1(1个结点) = 6
- 总比较次数:1+4+9+12+10+6 = 42次
- 平均查找长度:42 / 12(共12个结点) = 3.5
2.查找失败的平均查找长度
把二叉排序树的空结点补上,记录这个空结点对应的根节点是哪一层,有几个,然后按照上面相同的方法计算出总比较次数,最后除以空结点个数,得出平均查找长度。
视频链接: 二叉排序树的查找分析(青岛大学-王卓)
考点4 哈希表
此部分教程P350例题9.9和P356例题9.11要看懂
不知道什么叫哈希表的同学,先看下面这个视频。
视频链接: 哈希表的基本概念(青岛大学-王卓)
一、哈希冲突的解决办法——线性探测法
注意弄懂书上P350例题9.9,我觉得挺简单的,就不讲了。
看不懂就看下面这个视频。
视频链接: 线性探测法(青岛大学-王卓)
二、计算哈希表的平均查找长度
1.查找成功的平均查找长度:将哈希表中的探测次数相加/元素个数。
例如书上P356的表9.2,查找成功的平均查找长度,就是将探测次数加起来,除以元素总个数7个。
2.查找失败的平均查找长度:计算查找失败有点复杂,不太好用语言描述,我叙述一下书上P357的表9.3的探测次数是怎么来的。
首先和H(K)=0(下标0)开始查找比较,然后是比较一次,关键字不相等,然后和下标1 2比较,都不相等,比较3次,因为下标2的关键字是空,所以比较3次确定比较失败,下标0的探测次数为3。
然后是和H(K)=1(下标1)比较,紧接着比较下标2, 比较2次,因为下标2是空,所以比较2次确定比较失败,下标1的探测次数为2。
类似的对H(K)=2(下标2)比较,因为下标2本身就是空,比较1次确定比较失败,下标0的探测次数为1。
后面以此类推,因为一共只有7个元素,所以最大与下标为6的元素进行比较。
最后将将哈希表中的探测次数相加/元素个数,就是查找失败的平均查找长度。




5 Comments
哎哟,不错嘛?
good
??
很不错哟
没有排序吗哥们